合成シリカの物性を評価するためには、表面積(比表面積)が重要な指標の一つとなります。
今回は、合成シリカと比表面積の関係について、BET吸着理論を中心に解説します。
表面積と比表面積
表面積とは
表面積とは、立体を形成する全ての面の面積を合計した値です。地面と接している底面も含む、立体が空気に触れている外側の面の面積を全て足した値や、立体を展開してできる「展開図」の面積の値など色々な言い方がされます。紙を切り貼りして立体を作るときに必要な紙の面積の合計といってもいいでしょう1)。
球の表面積・体積
詳細については後ほど解説しますが、吸着法の主流であるBET法で比表面積を測定するとき、微小の球状分子を個体表面に吸着させてその吸着量から比表面積を算出します。したがって球の比表面積、体積は比表面積測定には大切なファクターとなります。
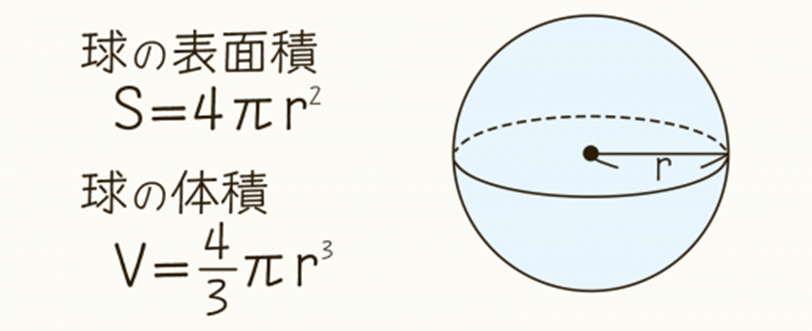
Fig1. 球の表面積と体積の公式2)
Fig2に個体表面における吸着分子(球状)の吸着イメージを示します。この場合、個体表面に51個の吸着分子があります。球の比表面積を1nm2と仮定すると、この個体表面は51nm2の表面積を有していることとなります。
合成シリカのような粒子が細かくナノサイズの細孔を有している固体材料を測定するためには、ナノサイズの粒子を用います。1nmは10-9mなので1nm2は10‐18m2となり、非常に小さいもので、この粒子径が小さいほど誤差が少なく正確な測定が可能となります。
ちなみに、表面積測定によく用いられる窒素分子の表面積(分子占有面積)は0.162nm2で、非常に小さな粒子となります。
また、窒素のほかにアルゴン、ヘリウム、n-ブタン、ベンゼンなども使用されますが、分析コスト、ガスの取り扱い等を考慮した場合、特殊な用途以外は吸着質には窒素が用いられています。
Table1 窒素ならびに吸着質各種の分子占有面積3)


Fig2.個体表面における吸着分子(球状)の吸着イメージ
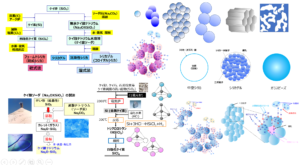
合成シリカの表面積
Fig3にヒュームドシリカ、シリカゲル、沈降性シリカの構造と表面積の関係を示します。
ヒュームドシリカ、沈降性シリカは、細孔を有していないため表面積は粒子の表面を測定していることになります。一方、シリカゲルは細孔が存在しているため、細孔の外側が外部表面積、細孔の内部は内部表面積と分類することができます。
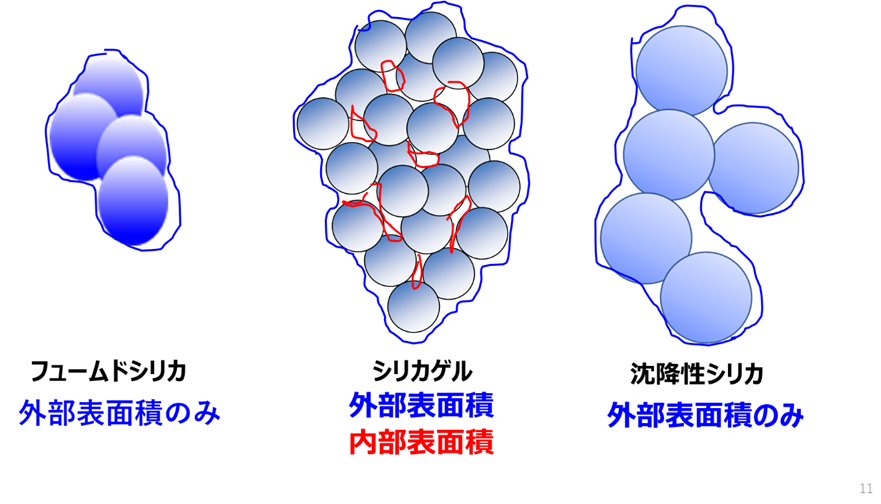
Fig3. おもな合成シリカの構造と表面積の関係
しかし、フュームドシリカや沈降性シリカのように細孔を持たない合成シリカも、たくさんの粒子が集まる凝集により細孔が生じます(Fig4)。
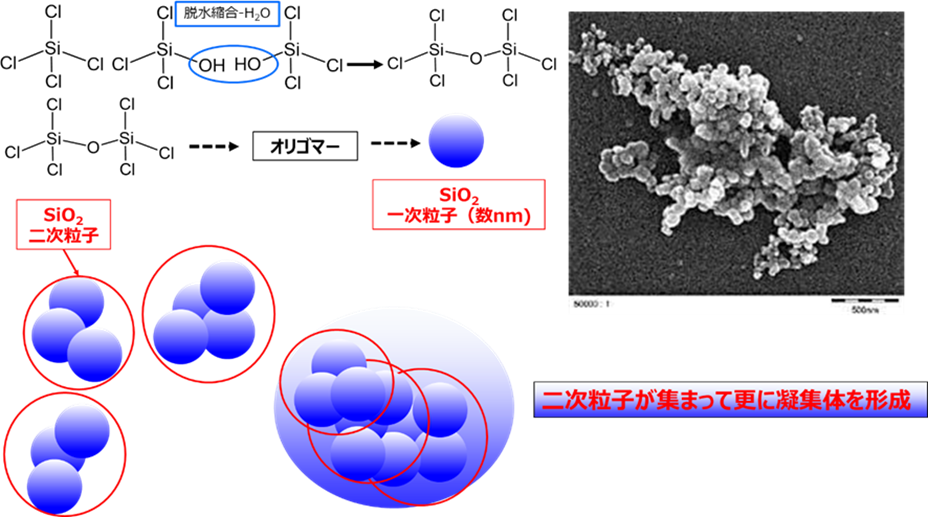
Fig4.ヒュームドシリカの構造と凝集
このため、表面積の測定値からは内部表面積、外部表面積の区別ができませんが、電子顕微鏡画像から算出した比表面積と比較することで内部比表面積の有無を確認できます。
Table2.フュームドシリカの一次粒子径と比表面積の関係4)

窒素吸着法(BET)による比表面積は、内部比表面積と外部比表面積を合わせた値、一方、電子顕微鏡法による比表面積は画像測定のため、外部比表面積を表していることになります。
ヒュームドシリカAの一次粒子径(個数平均)40nmの窒素吸着法(BET)による比表面積は50 m2/g、電子顕微鏡法による比表面積は45 m2/gという結果から、比表面積の割合は外部90%、内部10%となり、ほとんどが外部比表面積に占められていることになります。
また、一次粒子径が小さくなることにより遮蔽効果が大きくなるため、外部表面積の占める割合は小さくなる傾向があります。しかし、ヒュームドシリカDの一次粒子径(個数平均)8nmでも、外部比表面積の割合が8割程度占めていることになります。
比表面積
合成シリカのような粒子が細かくナノサイズの細孔を有している固体材料の表面積は、非常に大きくかつ、表面積のままで他のものと比べるのは非常に難しいものとなります。このため、重さ(単位質量)あたりの表面積や体積(単位体積)あたりの表面積で表します。
この単位体積や単位容積で表した表面積を比表面積といい、1g当たりの表面積(m2/g)や(m2/cm3)で表され、比表面積が大きいほど「粒子が細かい」ことを意味します。
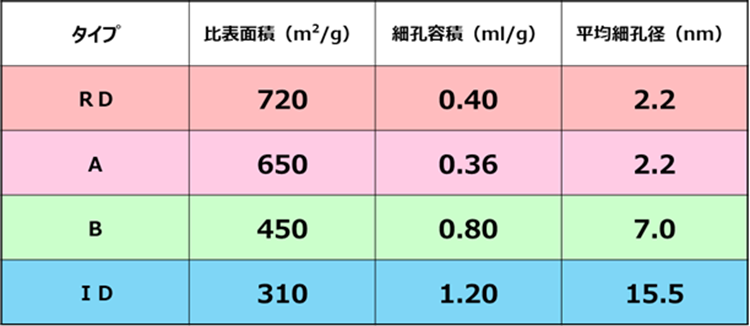
合成シリカには比表面積が規定されており、シリカゲルの場合はTable2のように、細孔容積、平均細孔径とともに4つのタイプに分類されます。
Table2. シリカゲルの各タイプと代表物性値
比表面積測定値は、合成シリカの特性や品質を直接表すことができる重要なデータとなります。
比表面積測定法
比表面積の測定法には以下に示すような様々な方法が存在して、おおまかには透過法、気体吸着法に大別されます。

Fig6.比表面積の測定方法5)
透過法
粉体の充填層に流体(水、空気等)を流す時、粉体粒子が細かいほど流れにくくなります。粉体の粒径と流体の透過性との間には相関があります。この関係から粉体の比表面積を求めようとするのが透過法です。透過法の基礎になっているのがKozeny-Carmanの式です。適当な試料筒に充填した粉体層に流体を通し、そのときの圧力降下と流速を測定すると、試料の比表面積が求められます。求められる比表面積は外部比表面積であって流体の流れに影響しないような亀裂や細孔内の内部表面積は測定されないため、合成シリカのような細孔を有する粒子には不適です。
気体吸着法
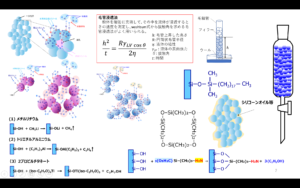
粉体粒子より十分小さく、かつ大きさが既知の小球を粒子の表面に隙間なく並べてその個数を数え、小球一個が占める六角形の面積を乗じてやれば比表面積が求められます。通常この小球として、窒素などの気体分子が用いられ、これを試料表面に隙間なくならべるために、吸着という現象が利用されます。
この方法は、外部表面積、内部表面積ともに測定ができるため、合成シリカのような細孔を有する粒子の測定に用いられます。
物理吸着法
固体(粉体)に対する気体分子の吸着現象には吸着様式の違いから、物理的引力による物理吸着と化学的引力による化学吸着に分けることができ、表面積測定には通常物理吸着が用いられます。
更に、物理吸着は検出方法の違いから、容量法、重量法、流動法に分類されます。
容量法
吸着前後のガス分子数の変化から吸着量を求めるものです。理想気体の状態方程式を利用する方式で、定容法は一定容積内の圧力変化を検出する方式で、定圧法は一定圧力にするためのガス導入量を検出する方式です。
重量法
吸着による試料重量の増加を直接検出する方式です。比表面積を窒素吸着法で測定する場合の必要感度を例に考えると,単分子層吸着したときの質量が 0.286 mg/m2 であることから,比表面積が数 m2/g 以上ある微粉でないと通常の電子天秤での測定は難しく、水や他の蒸気など重量変化の大きな物質の吸着量測定に適しています6)。
流動法
吸着ガスとキャリアガスの混合ガスを流し、吸着時の混合比を検出する方式で、吸着ガスを適当なキャリアガスに混合して試料粉体容器に流し吸着させてその濃度変化を測定する方法をいいます。
濃度の検出はガスクロマトグラフに利用される熱伝導度セルなどを用いる装置が多く、キャリアガスには He、吸着ガスに N2 を用いるのが一般的で、Nelsen法と溶出法があります。
Nelsen法は、混合気体を流している試料セル部分を液体窒素で冷却し,吸着による N2 ガスの濃度変化を記録する連続流動法です。
溶出法は、吸着条件にセットした試料容器中に流しているキャリアガスに吸着ガスを混合して吸着平衡に達したあとに吸着ガスを止めてキャリアガスで吸着ガスを溶出させ、その濃度変化を測定する方法です。流動法では吸着ガスの保持時間や保持容量の温度依存性から吸着熱を求めることもできます7)。
BET法
BET法は気体吸着法の一種で、ほとんどの物質は、非常に低い温度にさらされると、周辺に存在するガスの分子をファンデルワールス力によってひきつける傾向があります。これを物理吸着(ガス吸着)といい、比表面積測定に用いられる原理です。
BET法とは、ある条件下において、粒子を低温状態にした時に粒子表面に物理吸着したガス量を測定し、比表面積を計算する方法で、Langmuir が提唱した単分子吸着理論を拡張し、多分子層吸着理論に拡張したものです。この計算式を導き出したのがBrunauer 、 Emmett 、 Teller の 3 名で、頭文字をとって BET 法と名づけられました8)。
BET吸着等温式
BET理論は表面に分子が吸着できるサイトが存在し、それらのサイトに分子が多層に吸着するモデルを考えています。このモデルにおいて、0,1,2…i 層まで分子を吸着しているサイトの数をそれぞれ S0, S1,S2…Si とする。S0=1 とは分子をまったく吸着していないサイトが1つ、S5=3 は5層目まで吸着しているサイトが3つあることを示しています。

Fig7.多分子層吸着モデル
まず、吸着平衡状態では(i-1)層に入ってくる分子の吸着速度と i 層の分子の脱着速度は等しいと仮定します。
吸着は分子が壁にぶつかったときに起こると考えるとその速度は単位時間あたりにぶつかる分子数に比例し、吸着しようとしている層のサイト数にも比例すると考えられる。分子運動論によれば単位時間あたりに壁にぶつかる分子数 n は圧力 p と温度 T により
$$
n \propto \frac{P}{\sqrt{T}} (1)
$$
となるので、温度が一定のときは圧力に比例することがわかります。一方で脱着速度についてはi層目の吸着エネルギー𝑄𝑖により
$$
\exp \left(-\frac{Q_{i}}{R T}\right) (2)
$$
に比例する。よって、これら二つの速度が等しくなるとき
$$
a_{i} p S_{i-1}=b_{i} S_{i} \exp \left(-\frac{Q_{i}}{R T}\right) (3)
$$
が成立します。
全吸着量はiSiをすべて足し合わせたものであるので
$$
N=\sum_{i} i S_{i} (4)
$$
また単分子層吸着量はSiをすべて加えればよく
$$
N_{m}=\sum_{i} S_{i} (5)
$$
となる。ここで計算を簡単にするために2 層目以上に吸着した分子の吸着エネルギーは潜熱に等しいと仮定すると(6)式が導かれます。
$$
Q_{i}=Q_{L} \quad(i \geq 2) (6)
$$
また、2 層目以上では吸着に与える表面固体の影響は小さく、主として吸着分子間の相互作用によって吸着するとして、定数の比は変わらないため(7)式となります。
$$
\frac{a_{i}}{b_{i}}=g=\text { const } \quad(i \geq 2) (7)
$$
とする。
さらに(8)のように変形すると
$$
\begin{gathered}
\left(\frac{p}{g}\right) \exp \left(\frac{Q_{L}}{R T}\right)=x \\
\left(\frac{a_{1} g}{b_{1}}\right) \exp \left(\frac{Q_{1}-Q_{L}}{R T}\right)=\mathrm{C} (8)
\end{gathered}$$
(4)式より
$$
\begin{aligned}
N & =\sum_{i} i S_{i} \\
& =S_{0} \cdot \frac{C p}{g} \exp \left(\frac{Q_{L}}{R T}\right) \cdot\left(1+2 x+3 x^{2}+\cdots\right) \\
& =S_{0} \cdot \frac{C p}{g} \exp \left(\frac{Q_{L}}{R T}\right) \cdot \frac{1}{(1-x)^{2}}(9)
\end{aligned}
$$
一方(5)式より
$$
\begin{aligned}
N_{m} & =\sum_{i} S_{i} \\
& =S_{0}+S_{0} \cdot \frac{C p}{g} \cdot \exp \left(\frac{Q_{L}}{R T}\right) \cdot\left(1+x+x^{2}+\cdots\right) \\
& =S_{0} \cdot\left[1+\frac{C p}{g} \cdot \frac{\exp \left(Q_{L} / R T\right)}{1-x}\right] (10)
\end{aligned}
$$
が得られ、これらから
$$
\frac{N}{N_{m}}=\frac{C x}{(1-x)(1-x+C x)} (11)
$$
となります。
このモデルでは吸着層数が無限大まで可能であると仮定されているため、飽和蒸気圧での 吸着層数が無限大になります。
となる。このモデルでは吸着層数が無限大まで可能であると仮定されています。すなわち飽和蒸気圧での吸着層数が無限大になります。したがって飽和蒸気圧P0においてX=1となります。
(8)式より
$$
x=\frac{p}{p_{0}} (12)
$$
になります。
実用上は(11)式を
$$
\frac{P}{N\left(p_{0}-p\right)}=\frac{1}{C N_{m}}+\frac{C-1}{C N_{m}} \cdot \frac{p}{p_{0}} (13)
$$
として相対圧に対してグラフをつくり直線の傾きと切片から定数 C 、Nm を求めます。ただし、直線になる のは 0.05 ≤p /p0≤ 0.35 程度の範囲なので、実際はこの範囲で測定を行う。測定によって得られたグラ フから傾きと切片を求め、これにより表面を 1 層覆うのに必要な物質量𝑁𝑚を求めることができる。分子 一個が占める表面積を a とすればアボガドロ数𝑁𝐴を用いて測定したい表面積は S = a × 𝑁𝑚 × 𝑁𝐴 から求めることができます。9)
BET比表面積測定法
BETによる比表面積の測定は、連続法(多点法)と一点法に分類されます。
連続法
Fig6に連続法の概略図を示します。
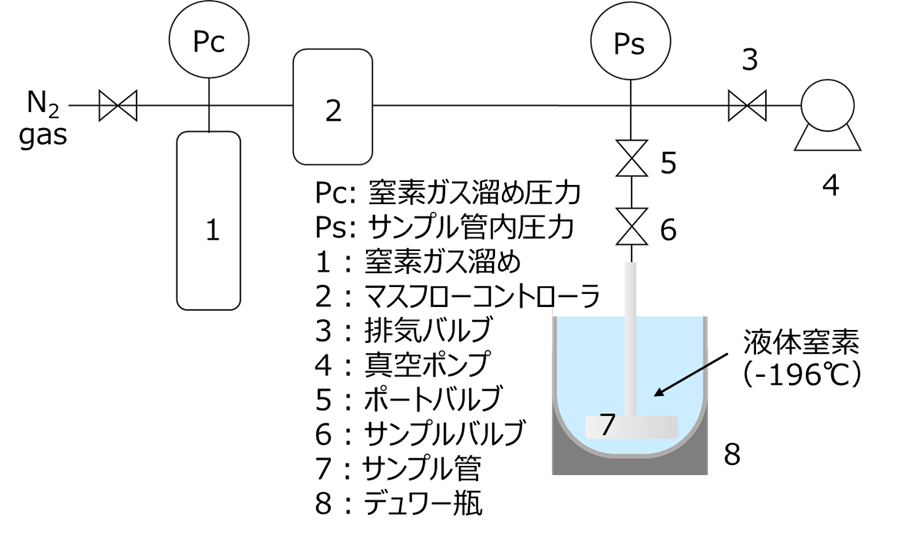
窒素ガス溜めVcに窒素を導入し、次にマスフローコントローラーにより一定質量を液体窒素浴中のサンプル管(容量既知Vsに導入します。このときの窒素ガス溜めの圧力Pcの変化と、サンプル管圧力Psの変化からサンプル重量当たりの吸着量が求められます。
このとき、窒素ガス溜めの死容積をVc 、サンプル管の死容積をVsとすると、サンプル管圧力Pstにおける吸着量Vは以下の式により求めることができます。
死容積とは冷却されているところの体積を装置温度(室温)に換算したみかけの体積です。
$$
V\left(P_{s t}\right)=\frac{V_{c}\left(P_{c o}-P_{c t}\right)-V_{S}\left(P_{c o}-P_{s o}\right)}{\mathrm{W}}
$$
Pco: 吸着開始時ガス溜め圧力
Pct:サンプル管圧力Pst時のガス溜め圧力
Pso: 吸着開始時サンプル管圧力(通常はゼロ)
連続法の特徵は以下の通りです。
- 連続測定のため測定デー多非常に多い
- 圧力変化のみ測定
- 吸着量を単純な圧力変化で算出するため、演算方式に比べて制度が高い
- 連続ガス導入のため、真の平衡吸着圧を測定していない
BETチャート
チャートとは、情報の視覚的表示、図(もしくは図を並べた表)・グラフ等のことで(語源はCardと同じくパピルス紙を意味するラテン語のChartaが由来です。10)
BETチャートとは、BET測定で得られた吸着等温線、BETプロット等のデータが記載されている図表になります。
吸脱着等温線
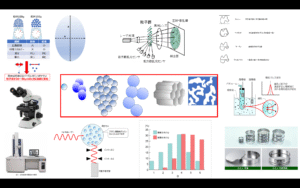
圧力を変化させ、そのときの吸着量を測定し、その結果を、横軸に相対圧、縦軸に吸着した量をとってプロットしたものを等温線(isotherm)と言います。特に圧力増加の方を吸着側等温線、圧力減少の方を脱着側等温線というように区別します。
吸脱着等温線は、比表面積をもとめる他、細孔容積や細孔形状の情報を得ることができます。
Fig7にB形シリカゲルのBET吸着等温線を示します。
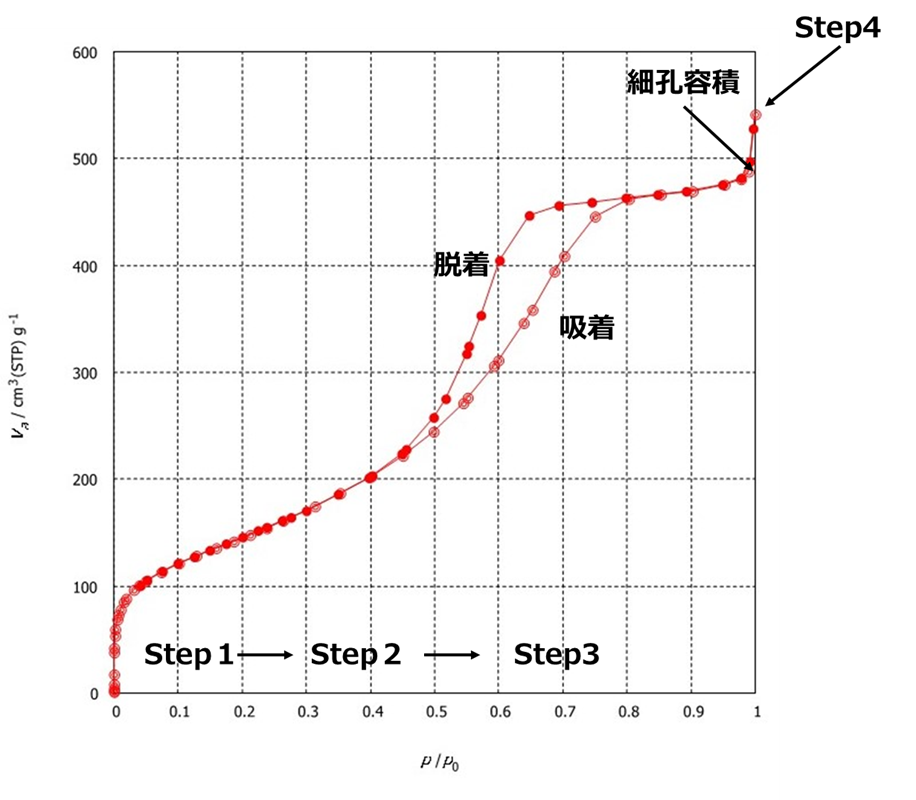
Fig9.B形シリカゲルの窒素吸脱着等温線(77K)
吸脱着等温線は、温度、吸着物により変わるため、かならず吸着物と温度を示さなくてはなりません。今回は-197℃(77K)における窒素の吸着等温線となりますので、“窒素吸脱着等温線(77K)”と示しています。
Step1の定圧領域から、圧力の上昇にともないStep2→Step3を経てStep4に至り、最終的に圧力比(p/p0)が1.0のときには吸着量は最大となります。Step2では窒素分子が1層しか吸着していないため、この状態から窒素分子数、窒素の占有面積と試料量から比表面積を求めることができます。
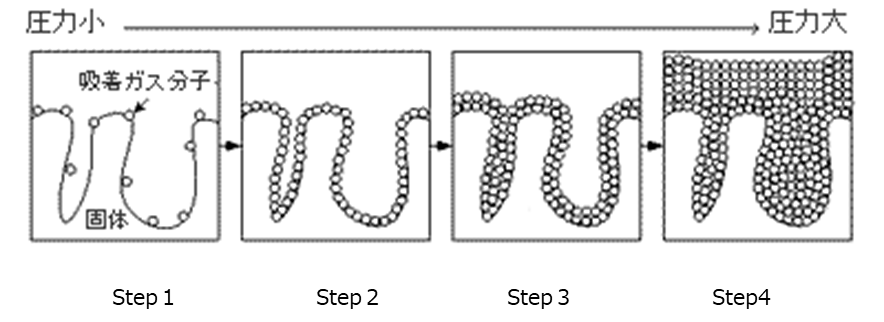
Fig10. BET吸着プロセスと細孔の状態(イメージ)11)
細孔の情報
細孔容積は、吸脱着等温線の飽和しているところの相対圧と窒素吸着量から求められます(Fig9)。また、吸着に加えて脱着も測定していますので細孔の形状を検討するための情報も得られます。Fig7は吸着と脱着の圧力差(ヒステリシス)が見られます。これはFig12のように、B形シリカゲルがメソポーラスシリカの筒形の細孔構造と異なり、網目状の細孔構造を有していることを表しています。

Fig11.細孔の飽和状態12)

Fig12.メソポーラスシリカとB形シリカゲルの細孔構造とガスの流れ(イメージ)
吸脱着等温線から比表面積の算出
繰り返して述べますが、比表面積は吸脱着等温線から、Step2の第1層吸着の状態からその吸着分子の占有面積と個数かと試料量から求めることができます。BET吸着等温式により第1層吸着の状態を見極めます。
$$
\frac{P}{N\left(p_{0}-p\right)}=\frac{1}{C N_{m}}+\frac{C-1}{C N_{m}} \cdot \frac{p}{p_{0}} (13)
$$
(13)のBET吸着等温式(BET式)は次のように変形できます。
Vmは単分子吸着量を表しています。

この式は一次式(Y=ax+b)で表すことができます。
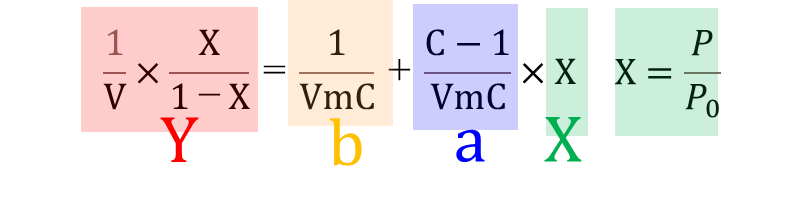
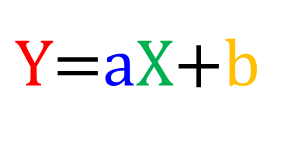
この一次式から以下のようにプロットすることによりBETプロットチャート(プロット)が得られます。

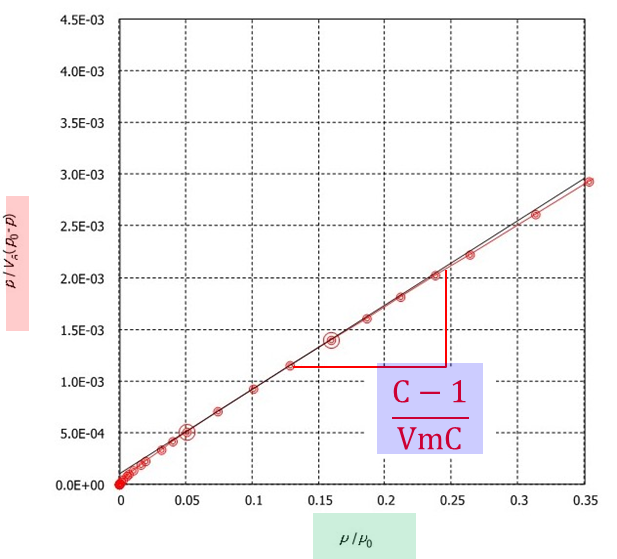
BETプロットは縦軸(p/VA(p0-p))に横軸に相対圧をとり、横軸(p/p0)は相対圧、傾きXはC-1/VmCなります。
このBETプロットにからVm、Cを算出し、以下の式とサンプル量から比表面積を求めることができます。
$$S_{B E T}=\frac{V_{\mathrm{m}}}{22414} \cdot 6.02 \times 10^{23} \cdot \sigma \cdot 10^{18}$$
Table3にFig11のBETプロットより求められた測定結果を示します。
Table3. BETプロットからの測定結果

Vm、Cから求めた比表面積SBETは528m2/g、全細孔容積(細孔容積)は0.7577となり、このときの相対圧(p/p0)0.9900は、細孔中に窒素分子が充填されたときの圧力(飽和圧力)となります。
また、今回は詳しくは解説しませんが、細孔径分布や細孔直径を求めることができます。
また、BET測定を行うにあたり高真空が要求されるため、測定開始の真空圧力は0.4459paとなり、非常に高い真空状態からスタートしています。
C値
Cは別名C値といい非常に重要な数値です。Cは、吸着第1層と第2層以降の吸着熱の差を示すパラメータになります。C>2であれば等温線はII型もしくはIV型を示し、そうでなければIII型もしくはV型を示します。Cが大きければ大きいほど低圧部の曲線部分と中圧部の直線部分の境目が明確になります。この点はB点とも呼ばれ、単分子層吸着と多分子層吸着の変わり目を示しています。
窒素ガスを液体窒素温度で吸着させる場合、0.01~0.05の適正な相対圧範囲においてCは50~300程度の値を取ります。このとき、比表面積が500m2/g以上でCが300以上になるときは、細孔が窒素分子より小さい(マイクロポア)の内部に窒素分子が入らないことが原因です。
また、C値がマイナスを示すことがあり、この場合は窒素分子が凝縮してしまったことが原因で、いずれも窒素分子として細孔内に入らないこととなります。
このような場合、BET法による比表面積は真値を示しているとは言えなくなるため注意が必要です。

Fig13.C値と細孔の関係
BET法(一点法)
BET測定において、“吸着量は圧力0.05atmから0.3atmの間では表面積とほぼ比例関係”という性質を利用して測定する方法があり、この方法を一点法、別名簡易法、間便法といいます。
Fig12に一点法の装置概略図を示します。
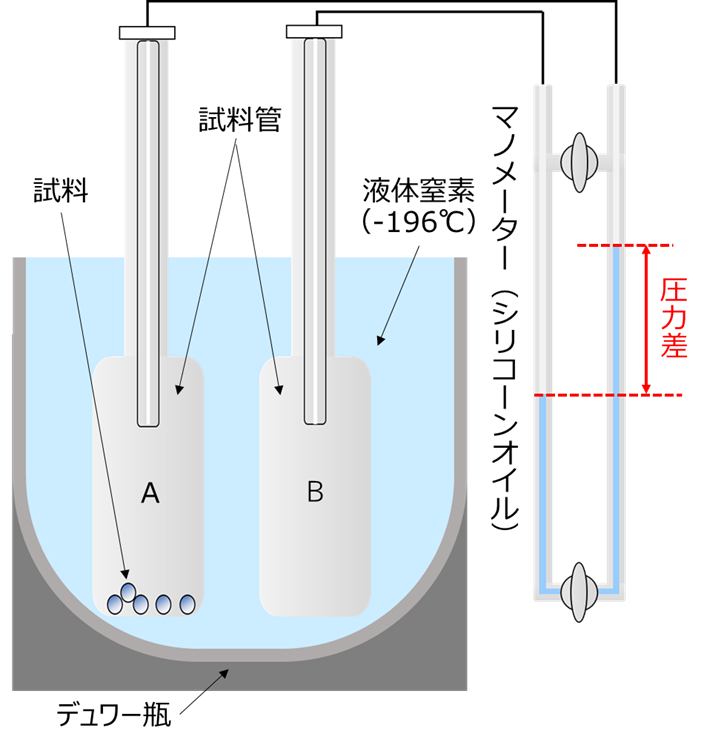
Fig14. BET法(1点法)の装置概要
試料管Aには試料が入っており、試料管Bはブランクとなります。試料管A、Bともに液体窒素に漬けて冷却させることにより、試料管のサンプルの分だけ窒素が吸着されて圧力が低下します。
圧力の低下により、試料が入って試料管Aと試料の入っていない試料管Bに圧力差が生じ、マノメーターの指示として現れます。このマノメーター指示とサンプル重量から吸着した窒素量が算出されます。
試料管内圧力と窒素吸着量より単分子吸着量を算出して表面積を計算することができます。
圧力0.05atmから0.3atmの間の適正圧力であるかは、以下のように検証することができます。
試料管内圧力は絶対温度(K)に比例します。
室温(25(℃)): 273+25=298(K)
液体窒素温度(-196(℃))=273-196=77(K)
P25℃ :25℃での圧力≒1atm
P-196℃:-196℃での圧力
P-196℃ =(77/298) × P25℃
P25℃は1atmよりP-196℃ =(77/298)×1
≒ 0.258 atm (0.05<P-196℃<0.3)
このときの圧力は0.258 atmとなり、適正圧力の範囲内であることがわかります13)。
比表面積測定の重要性
比表面積測定は、粉体原料や製品特性・品質をダイレクトに表す重要なデータとなります。また、合成シリカの他、化学工業で使われる反応触媒、コピー機のトナー、電池、インクなどさまざまな化学製品に表面積測定は欠かせません。
例えば、反応触媒は比表面積が非常に大きなものが要求され、1gあたり数百から1000 m2を超えるものもあります。一方、表面積の小さなものでは、球状粒子などがあります。材料や用途は様々ですが、粒子を球状に加工することによって様々なメリットが見出せ、例えばコピー機のトナーの場合、ボトルの中でブリッジを作って出てこなくなることを防止するために流動性を上げるために粒子を球状にします。更に、水酸化ニッケルやカーボンなどの電池の電極材料なども近年球状化が進んでいます。これは粒子を球形にすることによって電極の充填率を上げ、電気容量を向上させることが目的です。また、球状に加えて意図的に表面に細孔を持たせる(ポーラスにする)ことにより表面積が大きくなります。インクなどの色の元となる顔料などの発色材料では、表面積の大きさによって 色合いが変化します。同じ赤でも明るさや濃淡の違いは表面積の大きさによって大きく左右されます14)。
このため表面積は、研究所では新材料の開発や生産方法の確立など、工場では原料の受け入れ検査や最終製品の品質チェックなど、粉体を扱う現場では欠かせないデータとなります。 また、近年開発スピードに対する要求や、品質基準の強化に伴う測定精度への要求も年々に厳しくなっており、このような背景から、測定精度、測定スピード、容易な操作性、全自動運転が求められ、測定装置も日々進化しています。

Photo1. 表面積測定装置の一例15)
まとめ
合成シリカにおいて、比表面積は重要なファクターの一つとなります。比表面積はBET吸着理論を用いて測定されるのが一般です。BET吸着理論は、①第1層以外の全ての吸着層での吸着熱は、吸着質のモル凝縮熱と等しい、➁第1層以外での吸着・脱着の頻度因子は一定である、③飽和蒸気圧p0では、吸着質は固体表面上で凝縮し吸着層数は無限大となる。という3つ前提から成り立っています。このBET吸着理論より導出したBET吸着式から、第1層吸着状態とそのときの窒素吸着量をBETプロットから計算により求め、試料量から比表面積が求められ、更に細孔容積、細孔径、細孔径分布を求めることができます。このようにBET吸着測定から合成シリカの構造決定に必要な重要な情報が得られるため、不可欠な分析方法となります。また、このような理由から、BET測定は合成シリカばかりではなくさまざまな化学製品にも用いられています。また近年、製品の開発スピードや、品質基準の強化に伴う測定精度への要求も年々に厳しくなっており、このような背景から、測定精度、測定スピード、容易な操作性、全自動運転が求められ、測定装置も日々進化しています。
BET測定は、第1層以外の全ての吸着層での吸着熱は、吸着質のモル凝縮熱と等しい、第1層以外での吸着・脱着の頻度因子は一定であるという仮定のもとから成立しています。今後研究が進み、これらの仮定が解明されて更なる表面積測定が進化することを筆者は期待します。
参考文献
1)個別指導塾スタンダード https://std-ie.jp/tips/tip196.html
2)高校数学の美しい物語https://manabitimes.jp/math/968
3) A.L McClellan, H.F. Harnsberger, J. Colloid Interface Sci., 23, 577 (1967)
4)落合 満 エアロゾル研究 Vol.5 No.1 (1990) p. 34
5)島津製作所https://www.an.shimadzu.co.jp/service-support/technical-support/analysis-basics/powder/lecture/practice/p02/lesson01/index.htmlをもとに筆者作成
6)粉体工学用語辞典 http://www.sptj.jp/powderpedia/words/10961/
7)粉体工学用語辞典 http://www.sptj.jp/powderpedia/words/12529/
8)(株)マウンテック http://www.mountech.co.jp/product/teqcorner
9)近藤精一 石川達雄 安部郁雄 「吸着の科学 第3版」 丸善出版 pp. 32-35
10)Webio辞書https://www.weblio.jp/content/%E3%83%81%E3%83%A3%E3%83%BC%E3%83%88
11)島津製作所https://www.an.shimadzu.co.jp/service-support/technical-support/analysis-basics/powder/lecture/practice/p02/lesson04/index.html
12)島津製作所https://www.an.shimadzu.co.jp/service-support/technical-support/analysis-basics/powder/lecture/practice/p02/lesson04/index.htmlの図をもとに筆者作成
13)柴田化学(株)迅速表面積測定装置 SA-1000 取扱説明書
14)(株)マウンテック https://qr.paps.jp/i515o
15)マイクロトラック・ベル(株)https://www.microtrac.com/jp/products/gas-adsorption-measurement/surface-area-pore-size-distribution/belsorp-max-x/


-300x188.png)

-300x188.png)
-300x188.png)
コメント